Your complimentary articles
You’ve read one of your four complimentary articles for this month.
You can read four articles free per month. To have complete access to the thousands of philosophy articles on this site, please
Articles
Homo informaticus
Luc de Brabandere lets us sail with him along the two great rivers of thought that have flowed down the centuries from ancient philosophy into modern computer science, from Plato and Aristotle to Alan Turing and Claude Shannon.
The history of computer science did not begin eighty years ago with the creation of the first electronic computer. To program a computer to process information – or in other words, to simulate thought – we need to be able to understand, dismantle and disassemble thoughts. In IT-speak, in order to encrypt a thought, we must first be able to decrypt it! And this willingness to analyse thought already existed in ancient times. So the principles, laws, and concepts that underlie computer science today originated in an era when the principles of mathematics and logic each started on their own paths, around their respective iconic thinkers, such as Plato and Aristotle. Indeed, the history of computer science could be described as fulfilling the dream of bringing mathematics and logic together. This dream was highlighted for the first time during the thirteenth century by Raymond Lulle, a theologian and missionary from Majorca, but it became the dream of Gottfried Leibniz in particular. This German philosopher wondered why these two fields had evolved side by side separately since ancient times, when both seemed to strive for the same goal. Mathematicians and logicians both wish to establish undeniable truths by fighting against errors of reasoning and implementing precise laws of correct thinking. The Hungarian journalist, essayist and Nobel laureate Arthur Koestler called this shock (because it always is a shock) of an original pairing of two apparently very separate things a bisociation.
We know today that the true and the demonstrable will always remain distinct, so to that extent, logic and mathematics will always remain fundamentally irreconcilable. In this sense Leibniz’s dream will never come true. But three other bisociations, admittedly less ambitious, have proved to be very fruitful, and they structure this short history. Famous Frenchman René Descartes reconciled algebra and geometry; the British logician George Boole brought algebra and logic together; and an American engineer from MIT, Claude Shannon, bisociated binary calculation with electronic relays.
Presented as such, the history of computer science resembles an unexpected remake of Four Weddings and a Funeral! Let’s take a closer look.
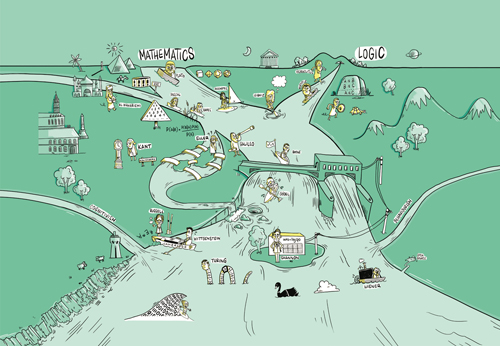
All images in this article powered by Cartoonbase 2020. “It’s not simple, it’s simplified”: Cartoonbase, creative agency artist: Martin Saive
Enlarge image
Algebra and Geometry
Arab mathematics came to the West during the Middle Ages. The arrival is important to our story because Al Khwarizmi (c.780-850) – from whose name we get the word algorithm – had invented a whole new way of doing calculations. Geometry had been the dominant paradigm since the Egyptians and Plato, but the Arabs demonstrated the principles and advantages of algebra. The Arabic mathematicians also brought the number zero along in their conceptual baggage. It’s difficult to imagine that the Romans hadn’t incorporated it into their numbers! How did they add up (say) XXXV and XV? How was the result, L, explained? But let’s not get side-tracked.
When Galileo (1564-1642) wrote that “the great book of the Universe is written in mathematics,” he put himself unambiguously in the tradition of Plato.
Galileo was a revolutionary in many ways. For instance, h e wrote in Italian, despite the fact than no European scholar had until then even considered abandoning Latin, the language of scholars. He was even innovative with his style, presenting Copernicus’ theory of a Sun-centred universe as a dialogue between a supporter and an opponent of Copernicus’ theories. A more fundamental innovation was that he used measuring instruments. Since ancient times, a long-standing tradition distinguished episteme from techne – knowledge from technology. Only technicians and engineers were supposed to get their hands dirty. The pursuit of knowledge by natural philosophers was supposed to progress by pure thought alone. Just as Vesalius decided to use a scalpel to show Galen’s mistakes, Galileo used a home-made telescope to show those of Aristotle. And he was right to do, since he then observed the phases of the planet Venus, the moons of Jupiter, and other phenomena that irrefutably proved Copernicus right and Aristotle wrong.
Descartes (1596-1650) reconciled geometry and algebra with his co-ordinate geometry. He invented the idea of graphs with x and y axes, unsurprisingly giving rise to Cartesian coordinates. His algebraic geometry was renamed ‘analytic geometry’, and still provides a tool for anyone wishing to design a curve. A circle can now be not only drawn, but also represented by the equation x²+y²=r², one form enriching the other. Descartes and his passion for mathematics has inspired geniuses to explore unknown territory. Some of them are included in the drawing.
The next important character in this story is Blaise Pascal (1623-1662). He led several lives; famous thanks to his book Pensées and the experiment that he organised at the Puy de Dôme to show the variation of atmospheric pressure, Pascal also built a remarkable calculating machine to help his father, and organised the first public transport system in Paris.
Amongst Pascal’s many lives, we will turn our attention to that of the inventor of probability calculus. Indeed, Pascal disputed the natural prevalence of Aristotle’s fourth cause – the idea that everything that happens in the world exhibits purpose – instead recognising the influence of chance. What’s more, he then wanted to calculate it! He used mathematics to prove, for example, that there are 11 chances out of 36 to score 6 by throwing two dice. Generally speaking, Pascal established laws that allow, with a given cause, the calculation of the probability of a given effect. He called his new discipline the ‘geometry of chance’. Slightly later on, Thomas Bayes (1701-1761), a particularly curious English pastor, decided to ask the question the other way around. Given an effect, he wondered, what is the probability of the cause? For example if I score 6 a number of times in a known number of dice throws, what is the probability that this happened because the dice was loaded? Today Bayesian theories on probability and statistics are widely used in the field of machine learning technology today are the basis for most recommendation algorithms on the internet.
This brings us to Leibniz (1646-1716), whose great dream is the cornerstone of this article. Bring together mathematics and logic? The German philosopher was convinced that it was possible. When involved in a disagreement, Leibniz apparently was often heard to say: “Well, let’s calculate!”
At the same time as Newton, with whom he didn’t confer (though they had a heated argument over priority), Leibniz laid the foundations of differential calculus, equations of the infinitesimally small which allow people to calculate about change, including change in motion. He was therefore able to prove that Achilles would always catch up with the tortoise, despite any head start he had given it. Two thousand years after he died, Zeno had met his match.
Like the philosopher Immanuel Kant, the mathematician Leonhard Euler lived in Königsberg in the eighteenth century. The city, known today as Kaliningrad, is structured around two islands, connected by seven bridges. The mathematician took different walks to try to cross each bridge once and only once, but he failed each time. His frustration blossomed into his interest in the science of networks we call topology.
Euler was not just a mathematician, he was also interested in logic, justifying even more his role in this story. He developed a graphical method to solve syllogisms, using circles that overlap. This approach is known today as the Venn diagram – once more illustrating Stigler’s Law, according to which no discovery carries the name of the inventor!
Kant’s own contribution to logic or mathematics is not decisive but he has earned his place in this story for at least two reasons. Firstly, in his Critique of Pure Reason (1781) he tries to shift the balance of knowledge between the objects that surround us and the subjects that we are, emphasising the importance of the subjective component, that is, the importance of the part played in knowledge by the knower herself. New areas of research then become possible, such as psychology. We will see the impact Kant’s insight will have in developing artificial intelligence.
Secondly, Kant said that part of his ‘Copernican revolution’ in knowledge involves recognising that we have an a priori idea of space. In short, according to Kant, if we can perceive an object, it’s because the object is in space and because this space is Euclidean.
Algebra and Logic
George Boole (1815-64) is in the centre of the fresco for good reason, because he’s the hinge between two worlds. He pushed Leibniz’s dream as far as possible, developing a method of working which tried to combine Aristotle’s logical syllogisms and algebra – in other words, to find the equations of reasoning! Such equations would allow us to verify a philosophical argument in the same way that we can prove a mathematical theorem.
Boole’s idea was pretty simple, to begin with. We speak of addition and multiplication in arithmetic, while in logic we speak of the function or and the function and. Why not try to combine both methods?
Consider two sets that overlap. If we take, for example, the set of wooden objects and the set of musical instruments, a stick only belongs to the first set, a trumpet only to the second, and a violin to both. Clearly, some elements belong to only one of the two: the set of wooden objects or the set of musical instruments. That illustrates the logical operation OR. The logical OR is like an addition in that we have to take into account the sum of both sets.
Others elements belong to both. That’s the logical AND: for instance, the set of wooden musical instruments. Boole wondered why the common portion shouldn’t be considered in terms of multiplication. His research led him to the equation x²=x, which is only arithmetically true for two values of x: 0 and 1. Binary calculation was therefore born a hundred years before computer science!
Bertrand Russell (1872-1970) started out as a logician. He addressed a problem which had been bothersome for over two thousand years – the paradox of the Cretan Epimenides, who stated that ‘All Cretans are liars’. Russell has his very own era. When he was born, there was no electricity in London; and by the time he died, Neil Armstrong had walked on the moon. This English aristocrat was intellectually ambitious and no respecter of established authority in logic or anywhere else. Of Aristotle’s logic, he wrote “Aristotelian doctrines are wholly false, with the exception of the formal theory of the syllogism, which is unimportant” (History of Western Philosophy, Book 1, p.202).
Russell persuaded his teacher Alfred North Whitehead to join him in a long-term project to provide a firm logical foundation for mathematics, basing it in set theory. The resulting three-volume book they called Principia Mathematica. A farewell to the logic of propositions, and welcome to the logic of relationships, it required a whole new nomenclature. But Russell and Whitehead’s adventure wouldn’t be a total success.
In 1931 a fuse blew. Kurt Gödel published his incompleteness theorem, wherein he proved that what is logically, undeniably true and what is mathematically demonstrable are two distinct things. So Leibniz’s dream would never fully come true, though much of practical use was being learned in the attempt. Even today, all computers are based around Boolean logic.
Binary Calculation and Electric Relays
Claude Shannon (1916-2001) provided the third great fruitful bisociation that structures our narrative.
Strangely, Shannon isn’t very well known. Even computer science professionals are often unaware of the crucial contribution he made to their field. But among other innovations, this American engineer decided to combine the binary system in logic/mathematics with the first electronic relays (they were lamps!) to create the first logic circuits.
Shannon also wanted to lay the foundations for an information theory. In particular he was interested in the laws governing the flow or transfer of information. Just as Nicolas Carnot theorised the workings of the steam engine into a science called ‘thermodynamics’, Shannon searched for the laws and principles that governed computer operations. Indeed, just as the scientists working on thermodynamics originally did so because they sought to optimise the working of steam engines, Shannon sought to optimise the transmission of information along wires, and find the most efficient coding. In doing so he found surprising analogies using the concepts of ‘performance’ and ‘entropy’.
Black Box & Black Swan
So much for information theory, but what of artificial intelligence? Let’s start with the human mind. Psychology in the twentieth century saw two major flows (these appear on our river graphic, on the right and the left of the main stream). At first, the behaviourists led the discussion, convinced that the essence of human beings could be understood by analysing their observable reactions to stimulations. This ‘black box’ approach to the mind strongly inspired Norbert Wiener (1894-1964) when he started studying regulatory and steering mechanisms in a new discipline that in 1948 he named ‘cybernetics’. Wiener carefully studied the possibilities of automation. He is the undeniable forerunner of those who, nowadays, dream of intelligent robotics and artificial intelligence.
During World War Two, behaviourism slowly made way for a new perspective on human beings. Influenced by the IT metaphor, cognitivists believed that thought could be systematically modelled, and that reasoning broken down into a series of stages. Alan Turing (1912-54), who formulated the theory underlying modern computing, was certainly inspired by this way of seeing things. It motivated him to imagine a virtual machine, which he named after himself: a Universal Turing Machine, known these days as a computer.
You will have noticed that the cognitivists’ river runs on the left of the graphic, and the behaviourists’ on the right. This isn’t a coincidence. For Aristotle, knowledge is built first and foremost on experience. For Plato, on the other hand, knowledge relies primarily on reasoning.
Computer science has really taken off over the last fifty years. But all these new developments have continued to take place, as Newton would say, on the shoulders of giants – just as this overview underlines. What takes place today will become part of the continuity of the research which began in ancient times.
What will future computer science consist of? Different scenarios are argued for. For example, in August 2008, the technology-oriented magazine Wired announced that Big Data would result in ‘the end of science’! The thesis boils down to this: If we can gather billions of data, we no longer need equations, nor laws of causality, nor models – a knowledge of the statistical links is enough!
Aristotle stated that ‘science is knowledge of causes’. Could he have been outdone? For some, including Noam Chomsky – who is even more modern than ever – the answer is no. In an interview given to Philosophie Magazine in March 2017, Chomsky asserts that the challenge of science isn’t to establish an approximation of trends based on statistics, as the Wired article suggested. That would be like saying “We no longer need to do physics, we just need to film millions of videos of bodies falling and we can predict the falling of others.” Just as thousands of videos of dancing bees will not give us access to their language.
What will the future of computer science bring? I’ve learnt to be careful here. In 1984 I was a telecom engineer, and had read nearly all the forward-looking books on the subject. I wrote my book Les Infoducs while trying to think of all the options: the possibility of broadcast or interactive networks; slow or high speed, analogue or digital. I tried to think of everything… and I missed the most important thing, which was the advent of wireless technologies! Nowadays, we call this advent a ‘black swan’ – a very improbable event that has a very big impact. This is why a graceful palmiped of that colour is swimming peacefully along the river.
A lot of uncertainties… but one thing is nevertheless certain: Leibniz’s dream will never come true. But does this mean that the dream will turn into a nightmare?
There are reasons to worry. In Silicon Valley, a lot of conversations are centred around the ultimate (?) bisociation – one that would merge man and machine. But these discussions are between technicians and entrepreneurs. Very few societal or political thoughts are heard, and even fewer ethical considerations.
Everything is going faster and faster; but ultimately, is the internet our tool, or are we the tools of the internet? Who programs who? Who will write the Critique of Automatic Reasoning?
© Luc de Brabandere 2020
Luc de Brabandere is a fellow of the BCG Henderson Institute (BHI) and founder of the Cartoonbase agency. The main poster is available on request from Luc.de.brabandere@cartoonbase.com.
• This is a version of an article originally appearing in French in Philosophie Magazine in November 2016. The translator is Eve Wasmuth.