
Your complimentary articles
You’ve read one of your four complimentary articles for this month.
You can read four articles free per month. To have complete access to the thousands of philosophy articles on this site, please
Articles
Bad News for Fibophiles
Miriam Abbott says the Fibonacci series tells us nothing about the natural world.
Consider these facts:
a) ‘George W. Bush’ has eleven letters
b) There were 11 floors on each of the Twin Towers
c) September 11 is the 254th day of the year.
d) American Airlines Flight 11 was the first to hit the twin towers. It had 92 on board.
e) The second airplane to hit the towers had 65 on board
f) The lily has three petals
g) The violet has five petals
h) The dimensions of the Parthenon in meters are 30.88 by 69.5 by 13.72
i) At construction the Great Pyramid was 280 cubits tall and 440 cubits wide.
Any numerical fact becomes interesting when it’s significant – when it counts for something. The first five observations listed above are supposed to illustrate the significance of the number 11. For example, the fact that September 11 was the 254th day of the year is significant because 2+5+4 is also 11. That’s the pseudo-science of numerology1.
The last four facts, meanwhile, supposedly illustrate the significance of Fibonacci and Phi. And that’s considered legitimate science.
Most of us learn about the Fibonacci series and Phi in quick moments during a lecture on history or civilization. It’s introduced as a mathematician’s pattern that transcends the world of numbers. The pattern is found in nature and culture, it’s everywhere from trees to temples. It is mysterious, it is powerful, it is Phi.
Well, yes. And no. While Phi and Fibonacci are interesting and perhaps even mysterious, their scientific bearing is mostly myth. Introducing the series as anything more than a mathematical event crosses the line from science to numerology.
Fibonacci Found
Fibonacci (aka Leonardo of Pisa) was a mathematician who lived during the 12th century. It was he who identified the famous sequence that begins 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. After the first two values, each number in the series is generated by adding the preceding two; for example, the number 89 is the sum of 55 and 34. The relationship that holds between each number and its successor approximates an irrational number called Phi, 1.6180339887....
Equally important is this number, Phi. References to it date back as far as Euclid (c. 325 BC–265 BC)2, and it’s also known as ‘the golden ratio’, ‘the golden section’ and ‘the golden mean’. Phi is the ratio created when a line is divided in such a way that the relationship between the larger segment and the entire length is the same as the relationship between the smaller and larger segments (illustration below).
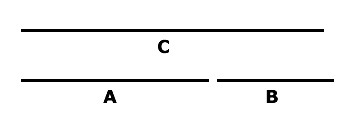
The length of C would be A+B. When the ratio between A and C is the same as the ratio between B and A, then Phi has been achieved.
Natural Occurances
Fibonacci patterns are classically observed in the structure of pinecones, the seeds arrangement of sunflowers and in the shape of snail shells.
To find Fibonacci in a pinecone, one must look at the object in a fairly unconventional way. It’s not a matter of counting the scales, but rather counting the spiraled columns of scales that appear to run the length of the cone. In general, the number of columns is a Fibonacci number (frequently 8 or 13).
In much the same way, the pattern is observed in the growth patterns of sunflower seeds. The seeds appear to form in spiraling rows that emanate from the center of the bloom, again, the number of rows is almost always a Fibonacci number.
The numbers in the Fibonacci series can also be used to generate a curve called the golden spiral. As it winds outwards, this spiral becomes progressively looser – much like the shell of a snail. The similarity with the shell’s spiral pattern provides further proof of Phi’s influence on Mother Nature.
These three cases are the most frequently noted as proof of nature’s compliance with Fibonacci. There are also claims that the series governs the development of flowers, since almost all blooms have three or five petals. The human body is also supposedly built in accordance with the numbers; the human hand provides perfect fodder with five fingers, each divided in three sections by two knuckles. Five, three and two are all Fibonacci numbers.
These last claims, however, are far too flimsy to be considered evidence of Phi’s prevalence. It’s simply misguided to claim that most flowers have petals that correspond with the series – for example, the entire family of commonplace poppies have four petals3. As for the hand argument, it’s easily countered with the fact that we have only four fingers and one thumb.
Our Fibonacci Psyches
Beyond the world of science, it’s also been suggested that the Fibonacci series dominates human aesthetic sensibility. That an artist such as Leonardo Da Vinci instantiated Phi in his works is not surprising. His interest and commitment to mathematics was well documented.
When the Fibonacci ratio is found in the architecture of Ancient Greece and Egypt, on the other hand, it’s another story. How did Phi manage to appear in architecture before it was discovered?
It seems quite mysterious that way back in 2575 BCE, Egypt’s Great Pyramid was built 440 cubits wide and 280 cubits tall. Divide the width by the height, and the resulting number is close to Phi.
Phi can again be found by using the Pythagorean theorem. Given a right triangle drawn using the pyramid’s slope, height and half-length, Phi would express the relationship between the Pyramid’s slope and half-width.
Finding Phi in the Parthenon requires more work. General texts about Western civilization suggest that the golden ratio is reflected in the façade4; the width appears to be Phi times the height.
Unfortunately, that claim is patently false. The width is more than twice the height. Phi is absent from any relationship between width (30.88 meters), height (13.72 meters) or length (69.5 meters)5. So Phi is identified in the Parthenon’s sections, and for Phi to be found, it must be unearthed in relationships that hold between the structure’s columns and trimming.
Bad News
Let’s address the architectural data first. If mathematics and science are fields in which accuracy counts, there exists a serious problem for Fibophiles.
First, the ratio of the pyramid is not Phi. It is 1.57. One would expect a force of nature to require closer compliance.
The second pyramid scenario is more mathematically sound, but quite contrived. Finding Phi only after performing a complex mathematical operation on the dimensions of the Pyramid is frighteningly close to numerology.
The math is worse for the Parthenon. Even if it’s divided in terms of column height (10.43 meters) and entablature (3.3 meters), we are nowhere close to Phi. The magical ratio can be found only in the distance between obscure architectural details, which doesn’t say much for Phi’s influence.
As for nature’s compliance with the series, Donald Simanek has generated wonderfully clear illustrations that demonstrate just how far Mother Nature’s shells are from the golden arc6. Both the golden spiral and a snail’s shell become wider with each revolution, but the resemblance stops there.
That leaves sunflowers and pinecones. Happily granted.
Given that Fibonacci’s original series was inspired by speculation about the population growth of a rabbit family in ideal conditions, and that pinecones and sunflower seeds are both modes for plant reproduction, let there be similarities.
Science versus Numerology
Scientific theories explain and predict phenomena. Pseudo-sciences such as numerology do not.
Fibonacci explains nothing, and it predicts only the number of spirals on pinecones and sunflowers. Fibonacci numbers are numbers, but numbers that don’t count in the world of science.
© Miriam Abbott 2006
Miriam Abbott is an Adjunct Instructor of Philosophy at Columbus State Community College. She is also a writer for The Other Paper (readership 285,900 in Columbus, Ohio).
Notes & Resources
1) These observations were collected from greatdreams.com
2) Mario Livo, The Golden Ratio, Broadway Books 2002.
3) Even more common are flowers with innumerable petals. It would be an interesting project to count the petals on flowers that typically generate more than ten – roses, carnations. Fibonacci fans have a distinct advantage when it comes to flowers with a handful of petals: the series comprises a majority of the numerals between 1 and 9.
4) For example, in An Incomplete Education, by Judy Jones and William Wilson, Ballantine Books 1995.
5) All Parthenon measurements come from metrum.org
6) Simanek’s dismantling of Fibonacci can be found at www.lhup.edu/~dsimanek/









