
Your complimentary articles
You’ve read one of your four complimentary articles for this month.
You can read four articles free per month. To have complete access to the thousands of philosophy articles on this site, please
Tallis in Wonderland
Thinking Straight About Curved Space
Raymond Tallis rules out a distorting physics metaphor.
In earlier columns, I have defended time from the assaults of physics. With a few exceptions, physicists have not been kind to time. Relativity theory stripped it of its tenses, dismissing the difference between past, present, and future as illusory. Worse, the theory seemed to deny time an independent existence. As Herman Minkowski put it, “space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union will preserve an independent reality” (The Principle of Relativity, 1952). Time in physics is present as an abstraction, a pure quantity: little t. This can be parked under a line as a denominator (e.g., speed = distance/t), or multiplied by itself, or by the square root of -1 – indignities that real stretches of time such as afternoons would not tolerate. And many physicists have dreamed of a version of a Theory of Everything in which time disappears altogether.
For some thinkers, notably the French philosopher Henri Bergson, the Original Sin is the presentation of time as if it were a kind of space. My own view, however, is that both space and time are traduced in physics. They should form a victim support group, which is why this column is devoted to a defence of space.
The most obvious assault on space is analogous to that which time has had to suffer: reduction to a pure quantity. Space is translated into points, lines, surfaces, and volumes; to dimensions or quantitative parameters x y, z. Places – habitats – are stripped down to decimal places. Much is lost in consequence. The space of the physicist has neither ‘here’ nor ‘there’, no centre or periphery, no inside or outside, except in terms of relationships between points defined mathematically with respect to a frame of reference built out of axes whose (0,0,0) point of origin is arbitrarily chosen. The inhabitants of the physicists’ space are fields and objects that have only primary qualities – size, distance, number of instances. They are void of secondary qualities – warmth, brightness, colour, texture – never mind meaning, value, and use – even though all these qualities are inseparable from the space in which we experience, enact, and suffer our lives.
Physicists would hardly waste a shrug on such criticism. The kind of space that they are interested in, the space of mechanics and of material objects and force fields, is not the parochial space of the shopper and the doctor and the tourist. Mechanics is not psychogeography; and a good thing too, they might argue. Its extraordinary explanatory, predictive, and practical power has come from shedding this irrelevant baggage.
So long as we don’t think that the physicists’ space is more fundamental than, or is the ultimate reality of, lived space, then no harm is done. Indeed, it might be argued that physical space should be grateful to modern physics for upgrading it from an inert background. The General Theory of Relativity brought the erstwhile backdrop, the stage set, into the drama, where space (and time) are active players. This is promotion indeed for an emptiness whose very existence was denied by our cognitive godfather, Parmenides (c.515-c.460 BCE). The Eleatic philosopher argued that since space was Nothing, it could not divide Being into beings: to be separated by Nothing was not to be separated at all, and the world seen aright was a single entity.

A radial picture of the Universe by Pablo Carlos Budassi
A Curve Ball At Curved Space
The price for promotion, however, is high: unintelligibility. For in contemporary physics, space is curved, or non-Euclidean. In non-Euclidean space, the sum of the angles of a triangle may be greater than 180°; more importantly, the shortest distance between two points may not be a straight line, but a curved one. Matter, it is asserted, warps space (strictly, spacetime): its gravitational field bends space (and dilates time). Any change in the amount and distribution of matter will change the curvature of spacetime. Euclidean geometry is the geometry of a space whose curvature is everywhere zero – the geometry of the imaginary space of a matter-free universe.
When we first hear talk of ‘curved space’ we rebel. The least we should ask of something said to be curved is that it should have edges, surfaces, and parts that look or feel curved, which space itself does not. Analogies are offered to make the idea less counter-intuitive. We are invited to think of a journey over the surface of the earth or any spherical object: the shortest distance between one point and another will inevitably be (or rather be represented by) a curved rather than a straight line. A straight line in the Euclidean sense doesn’t exist in curved two-dimensional geometry. And the sum of the angles of a triangle inscribed on the surface of a sphere will add up to more than 180°.
Those willing to think for longer than two seconds will see this explanation as a fudge. It is entirely possible, for example, to connect two points on the surface of a real spherical object such as the earth by a straight line, if you are willing to dig a tunnel. What’s more, while the earth may have a curved surface, it is not curved ‘through-and-through’, as curved space (which lacks surfaces) is supposed to be. The earth’s surface is curved, but within this surface, its substance, the material of which it is composed, is neither straight nor curved. That is why we can take straight or curved pathways through it.
Physicists will smile at taking the analogy too literally. But if it is not taken literally, it lacks explanatory force. And taken literally, it is seriously misleading. The curvature of an object such as the earth is extrinsic – evident in its surface. The putative curvature of non-Euclidean space is intrinsic: it is present at every level above that of an infinitesimally small spatial point. So resistance to the idea of curved space does not arise from a superficial misunderstanding that can be cured with the help of a simple analogy. Rather, it is resistance to the odd idea that emptiness can have any topology, curved or straight.
The Origin of Curved Space
So where does the notion of space having a curvature come from? Its immediate origin is in what Einstein described as his ‘happiest thought’. If you were in an elevator in outer space without reference points, and you felt a pressure under your feet, you could not tell whether this was because you had entered a gravitational field or because the lift was accelerating upwards. He concluded from this (and from the empirical demonstration of the equality of inertial mass – resistance to acceleration or deceleration – and gravitational mass) that there is no fundamental difference between gravity and other forces which cause change in velocity.
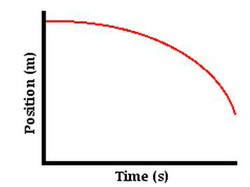
Graph showing the height of a falling stone against time
Consider now the path of an accelerating or decelerating body as it is often depicted graphically by physicists: it is a curved line. For instance, the representation of a falling stone’s position against time is a line that gets continuously steeper as the stone accelerates (see graph). Alternatively, circular motion is effectively continuously accelerating motion. Therefore, if acceleration and deceleration are ‘curved’, and gravity is identical to other inertial (accelerating or decelerating) forces, gravity can be seen as a force that bends the paths of objects as plotted against time. However, gravity is not local: it is a field, distributed throughout space. Hence a gravitational field becomes a space in which trajectories are curved, and space with a non-zero gravitational field is described as curved.
We are now in a position to understand the origin of the counter-intuitive – indeed unintelligible – notion of space being curved (or indeed, having any kind of topology). It arises from projecting into space our mathematical portrait of the influence of gravity on the trajectories of objects. However, by using an everyday term such as ‘curved’, we are conflating an appearance, as exemplified in the surface of a spherical object or the parabolic flight of a thrown missile, with a mathematical abstraction capturing the change in the position of an accelerated object with time. This is a prime example of what in The Concept of Nature (1920) Alfred North Whitehead called, “the muddle of importing the mere procedures of thought into the facts of nature.” In this case, we are translating handy ways of depicting (and hence predicting and calculating) the influences of gravity on the motion of objects (and indeed of light) through space – bending their trajectories – into the structure of space itself. Nevertheless, the fact that the mathematics of motion in space and the curved shape of graphs of position against time are congruent does not mean that space is itself curved, nor that it makes sense to say so.
The Distortion of Space
The unintelligible idea of ‘curved space’ is the product of misidentifying a system of representation with that which is represented. This habit has a long history. From Pythagoras onwards we have been prone to the illusion that our ways of geometrising space capture space itself – perhaps even believing that the mathematical logic of pure quantities is somehow ‘out there’. However, the immense power of mathematical physics – which requires abstracting from phenomenal reality and the reduction of experienced and experienceable reality to mere parameters to which numerical values are assigned – does not justify uncritically accepting concepts such as ‘curved space’ that attempt to re-insert phenomenal appearances into its abstractions. On the contrary, we should acknowledge that ‘unreasonably effective’ mathematics (to borrow Eugene Wigner’s phrase) can take us to places to which nothing non-mathematical corresponds. For instance, consider the assumption, central to modern cosmology, that space itself is expanding. It is not idiotic to be puzzled by the very idea of expanding space, given that ‘expansion’ is usually of stuff into relatively empty space. Thinking of emptiness expanding into something that is not even emptiness is more than a little odd.
Physics, and the technology based on it (and indeed our civilisation), has flourished by being prepared to set aside the common sense that tells us that the earth must be flat otherwise people will fall off it, that a small object will always fall slower than a big one, and that the state of rest and motion in a straight line are fundamentally different. But we should not conclude from this that the mathematical portrait of the world is the last word on what is really there, or that everyday experience of lived space is in some profound sense defective or even wrong.
In The Production of Space (1991), Henri Lefebvre, the ‘philosopher of everyday life’ reflected that, “Not many years ago, the word ‘space’ had a strictly geometrical meaning… In scholarly use it was generally accompanied by some such epithet as ‘Euclidean’… and the general feeling was that the concept of space was ultimately a mathematical one. To speak of ‘social space’, therefore, would have sounded strange.” We should recognise that the notion of ‘curved space’ is less legitimate than that of ‘social space’, however useful the former might be for the development of mathematical physics. And we should not be pressured into thinking that the space of daily life, which is neither Euclidean nor non-Euclidean, is somehow not the real thing.
© Prof. Raymond Tallis 2015
Raymond Tallis’s latest book is Summers of Discontent: The Purpose of the Arts Today with Julian Spalding (Wilmington Square). His website is raymondtallis.com.









