
Your complimentary articles
You’ve read one of your four complimentary articles for this month.
You can read four articles free per month. To have complete access to the thousands of philosophy articles on this site, please
Articles
Calling Time
Anthony Proctor asks: Are we on time? Do we have time? What is time?
Not only is time a long-standing mystery in itself, but it is also at the heart of many other mysteries, paradoxes, and misunderstandings. For instance, backwards time travel could lead to anomalies such as the famous ‘grandfather paradox’, where you go back in time to kill your grandfather, thus preventing your own birth. Or, time appears to progress, but we cannot ask ‘how fast?’ as there is no meaningful answer: one second per second is hardly a meaningful answer to the question ‘How fast is time flowing?’. And time is the only physical quantity that we can experience by thought alone, but when we do so, it sometimes appears to progress more swiftly, or more slowly, than at other times.
Even hundreds of years ago St Augustine was well aware of the problematic nature of time: ‘‘What then is time? If no one asks me, I know; if I want to explain it to a questioner, I do not know" (Confessions, c.400 AD). He also struggled to reconcile his theological beliefs with his experience of time, since even the creator of time cannot create in the absence of time, and yet if God exists in some ‘supertime’, then the problem arises of what was happening before God created anything at all, and if the answer’s ‘nothing’, then how could we say time passes there anyway?:
“But if the roving thought of someone should wander over the images of past time… let him awake and consider that he wonders at illusions. For in what temporal medium could the unnumbered ages that thou didst not make pass by, since thou art the Author and Creator of all the ages?”(Confessions)
Interestingly not a single equation anywhere in physics identifies our special ‘now’ moment, or even embraces dynamical change as we perceive it – apart from as a simple slope on a graph. This leaves us two choices: either time is non-existent (and all nows and dynamical changes are illusory), or mathematics cannot describe everything in the universe (and physics is doomed).
Experience vs Mathematics
On 6 April 1922, Albert Einstein took up a forum invitation to the Société Française de Philosophie in Paris to discuss his Special and General theories of Relativity. One of the many intellectuals there was the celebrated French philosopher Henri-Louis Bergson, who also wrote about time. The pair clashed at the event over the nature of time, and their heated debate turned into a lifelong disagreement on the subject. Like many readers of this article, Bergson believed in the basic reality of experience, and in a single universal time. He criticised Relativity for having distanced time from experience, thus leading to counter-intuitive consequences. Einstein had shown that space and time must be treated in a conjoined fashion mathematically, and that neither were absolute since their measurement depended upon the motion of the observer. But Einstein never bridged the gap between his mathematics and our first-hand experience of time. Such was Bergson's standing that his criticisms, could well have been a deciding factor that prevented Einstein receiving a second Nobel Prize, for Relativity. Physics now accepts that Einstein was right, but did Bergson have a point?
The truth is not so black and white. Before we can explore the different viewpoints – and explain how both missed an opportunity to answer many deep questions in philosophy and physics – we need to take a short tour of dimensions and spaces.
In popular culture a ‘dimension’ is synonymous with a separate reality or universe, as in ‘alternate dimension’ or ‘parallel dimension’, but this is an abuse of the term. A dimension is really an extent in a particular direction. It’s also useful to know that when we talk about spaces, their dimensionality indicates the minimum number of coordinates needed to specify any given location in that space. This would be three for our everyday space. It does not matter whether the coordinates are given in terms of some x, y, and z values relative to three axes at right angles, or in terms of a longitude, latitude, and distance from the centre of our Earth; there will always be three required. We consider space to be ‘flat’ or Euclidean, because it obeys Euclid’s basic geometric axioms, such as the angles of a triangle adding up to 180⁰ and Pythagoras’ theorem being correct. A sheet of paper is a two-dimensional Euclidean example. However the surface of a globe is a non-Euclidean, ‘curved’ space, upon which the angles of a triangle do not add up to 180⁰ .
How are we then to think about time in relation to physical space? Consider a moving ball A involved in a glancing collision with a stationary ball B. As any pool player will know, a glancing collision will send the balls apart, to the left and right of the incident path. Ignoring the possibility of any spin being placed on A, the angle of their separation is determined by simple conservation laws.
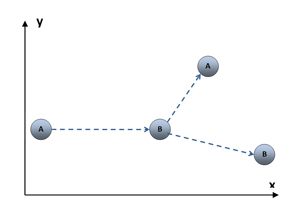
Collision in two dimensions
This diagram shows the collision in just two spatial dimensions: x and y. Time is not shown, but we can imagine A proceeding from left-to-right, hitting B, and then A and B bouncing off each other. But notice that we add that information to the diagram, which is otherwise entirely static in its depiction of the events.
But now imagine that we add time as a third dimension to this diagram. The collision then appears very different.
At the bottom this diagram shows the same two-dimensional spatial paths, but it also shows them as three-dimensional spacetime paths (x-by-y-by-t). We now see the actual speeds of the balls, which are represented by the gradients of the slopes of these pipe-like structures. However, the diagram is still entirely static, and the fact that A is travelling towards B is not implied by it. Again, we have to add information to our diagram to get that.
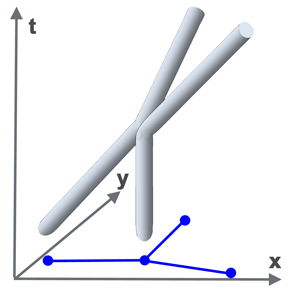
Collision in three dimensions
But now let’s imagine that these pipe-like structures are a picture of something real, and not simply implying motion on a spacetime diagram. In this situation, we no longer have to add any information because we are stipulating that the diagram fully captures the objective nature of A and B as structures that have an extent across the time dimension. This shows the idea of a block universe, in which all of space and time are a continuous single block.
When physicists talk about a block universe, they consider the point of view of a super-observer. You might interpret this as some god-like figure who resides outside of spacetime; but to a physicist, it is simply a hypothetical reference point from which to consider the whole of time and space together. However, those same physicists often fall into the trap of still adding the temporal information of movement, causality, and many other notions that we gain from our subjective experience – thus preventing them fully seeing the nature of the idea they’re using.
Einstein regularly used space-time diagrams to illustrate the motions of objects, but it was his former teacher, the German mathematician Hermann Minkowski, who reformulated the equations of Special Relativity using a four-dimensional notation where time is multiplied by the square root of minus one and the speed of light. By doing so, the equations then took on a much simpler form (as did many other equations in physics). And it is from this reformulation that we get the notion of a four-dimensional spacetime continuum. But one subtle implication of this mathematics was that time was a real dimension in the newly-minted ‘spacetime’, just like the spatial ones, and not merely an axis on a diagram. As a result, Minkowski's spacetime has since been used as a model for a block universe.
Misunderstanding Physics
When Einstein later formulated his theory of General Relativity (which explained the force of gravity in a very novel way), he extended Minkowski's spacetime from the ‘flat’ geometry of Special Relativity into a ‘curved’ or non-Euclidean geometry, within which objects affected by gravity are just following their natural paths through spacetime.
Unfortunately, the fact that both Minkowski's spacetime, and the spacetime in a gravitational field, are four-dimensional continua, has led to many misunderstandings and misrepresentations, not just in fiction but in philosophy and physics too. Writers regularly talk about objects travelling through spacetime, or through wormholes, or back in time, and so on; but in a block universe there is no movement, nor any dynamical change at all, because the contents are entirely static and immutable in the four spacetime dimensions. It would be meaningless to say that an object can move through a spacetime continuum; one only have to ask 'how fast?' or 'where is it now?' in order to see why. For instance, if an object were moving spatially from A to B, then you cannot meaningfully ask when it arrives at B in a block universe, since that time coordinate already exists, and hence from a block universe point of view it would already be there! This highlights that we can have no dynamical change without some special ever-changing time coordinate — a sort of ‘cosmic now' or dynamically changing present moment which progresses through time — and there is nothing in physics to even suggest that this exists.
The term 'wormhole' was coined by American theoretical physicist John A. Wheeler in 1957; but the correct term for the phenomenon is an Einstein-Rosen Bridge, after some work in 1935 by Einstein and Israeli physicist Nathan Rosen on solutions to the equations of General Relativity. A wormhole is essentially a shortcut from one remote point to another by joining the two remote locations together by ‘folding’ space, typically through gravity. Using the illustration of the two-dimensional surface of a sphere, imagine a depression on either side being forced together so that they connect. Now extend the illustration to be applying to a four-dimensional spacetime.
No one has ever seen a confirmed wormhole, and there are no observations that would benefit from such a description. A shortcut it may be, but there is nothing that could be construed as ‘travel’ because we’re talking about the 4D spacetime continuum of a block universe where there is no objective measure of dynamical change; that is, there is no movement. It’s just mathematics.
A related concept is a Closed Time-Like Curve (CTC) – a path that starts and ends at the same time coordinate: a sort of ‘time loop’. After Einstein moved to Princeton to work at the Institute for Advanced Study, he and Austro-Hungarian mathematician and philosopher Kurt Gödel became walking partners to and from the Institute. Gödel showed that CTCs could appear in certain solutions to the equations of General Relativity, leading to potential temporal anomalies; but he also rightly argued that Relativity itself left no room for a subjective flowing time, and that it must therefore be illusory, that is, in some sense, merely a mathematical model, however useful. Although the notion of CTCs is now routinely used to suggest a way of travelling back in time, Gödel's arguments would make that a nonsense, but his work on this subject is not well-known.

Experiencing Space & Time by Dror Rosenski 2022
Time In & Out of Mind
Why is this little tour of four-dimensional spacetime important?
The idea of a block universe can arguably be traced back over two thousand years, but it is not a popular idea because of its supposed repercussions for free will, causality, and all dynamical change. We accept that mathematics cannot address mental phenomena, such as emotions, thoughts, and perceptions: but perhaps it can be shown that all dynamical phenomena, including movement, are associated with the conscious perception of time. If so, then this leaves unobserved reality entirely susceptible to the mathematical description.
This approach can be summarised in two principles. Firstly a Temporal Anthropic Principle says that consciousness and subjective time cannot exist without each other; they are bound together as part of the same phenomenon. Secondly a Determinate Pattern Conjecture says that the pattern of changes over time in objective, unobserved reality can be fully modelled by sets of consistent mathematical axioms and formulae that are finite, deterministic, and continuous.
Using these principles it is possible to present a credible argument for the emergence of consciousness within a block universe, thus cleanly separating the objective reality of spacetime from the subjective experience of space and time. And this further means that all things that are independent of conscious observation must be susceptible to the mathematical description; and conversely, that all things not susceptible to such a description, must be a product of consciousness.
© Anthony C. Proctor 2022
Anthony C. Proctor is the author of On Time, Causality, and the Block Universe (2022). Website: parallax-view.com, email: parallaxview@proctor.net.









